Trees

Imports …

import pandas as pd
import numpy as np
from sklearn.metrics import accuracy_score
import plotly.express as px
import matplotlib.pyplot as plt
import plotly.io as pio
pio.templates.default = "plotly_white"

Example: Blood test for autism?

We’ll use an example from a 2017 PLOS Computational Biology paper. Download the data.

  • Typically autism is diagnosed by behavioral symptoms
  • If we could diagnose autism from a blood test, we could diagnose it earlier

The data has units on the second row, so we’ll skip that row.

autism = pd.read_csv("data/autism.csv", skiprows=[1])

We have 3 kinds of data about 206 children:

  1. The outcome (Group): ASD (diagnosed with ASD), SIB (sibling not diagnosed with ASD), and NEU (age-matched neurotypical children, for control)
autism.groupby("Group", as_index=False).size()
Group size
0 ASD 83
1 NEU 76
2 SIB 47

  1. The outcome (Group): ASD, SIB, NEU
  2. Concentrations of various metabolites in a blood sample:
```{python}
#| output: asis
print('\n'.join(f'- {column_name}' for column_name in autism.columns[1:-1]))
```
  • Methion.
  • SAM
  • SAH
  • SAM/SAH
  • % DNA methylation
  • 8-OHG
  • Adenosine
  • Homocysteine
  • Cysteine
  • Glu.-Cys.
  • Cys.-Gly.
  • tGSH
  • fGSH
  • GSSG
  • fGSH/GSSG
  • tGSH/GSSG
  • Chlorotyrosine
  • Nitrotyrosine
  • Tyrosine
  • Tryptophane
  • fCystine
  • fCysteine
  • fCystine/fCysteine
  • % oxidized
  1. The outcome (Group): ASD, SIB, NEU
  2. Concentrations of various metabolites in a blood sample
  3. For the ASD children only, a measure of life skills (“Vineland ABC”)
autism.groupby("Group", as_index=False).agg(mean_vineland=("Vineland ABC", "mean"))
Group mean_vineland
0 ASD 70.765957
1 NEU NaN
2 SIB NaN

Exploratory Data Analysis (EDA)

What do these metabolites look like?

autism_long = (
    autism
    .melt(id_vars="Group", var_name="Measure", value_name="value")
    .query("Group != 'SIB' and Measure != 'Vineland ABC'")
)
px.box(
    autism_long,
    x="value",
    y="Measure",
    facet_col="Group"
)

Exploratory Data Analysis (EDA)

EDA

  • This plot helps us compare different metabolites within each group.
  • Better question for predictive task: Which of these metabolites help us distinguish autism?

Approach:

  • easier to compare within a plot than across a facet, so switch y variable to Group.
  • absolute values don’t matter much, so let each metabolite have its own x scale.
  • plotly boxplots don’t show up well when small, so switch to a ridgeline plot
(
    px.violin(
        autism_long,
        x="value",
        y="Group",
        facet_col="Measure", facet_col_wrap=5
    )
    .update_traces(side="positive", width=3, points=False)
    .update_xaxes(matches=None)
    .for_each_annotation(lambda a: a.update(text=a.text.split("=", 1)[-1], font_size=10))
)

Can we predict ASD vs non-ASD from metabolites?

  • Let’s start by (1) ignoring the behavior scores (that’s an outcome) and comparing just ASD and NEU.
  • We need to drop SIB.
feature_columns = list(autism.columns[1:-1])
target_column = "Group"

positive_outcome = "ASD"
negative_outcome = "NEU"
data = (
    autism
    .query("Group != 'SIB'")
    [feature_columns + [target_column]]
)
print(data.shape)
(159, 25)

Train-test split

from sklearn.model_selection import train_test_split
train, test = train_test_split(data, test_size=0.25, random_state=123)
print("Training set shape: {}".format(train.shape))
print("Test set shape: {}".format(test.shape))
Training set shape: (119, 25)
Test set shape: (40, 25)

First Model: guessing most common

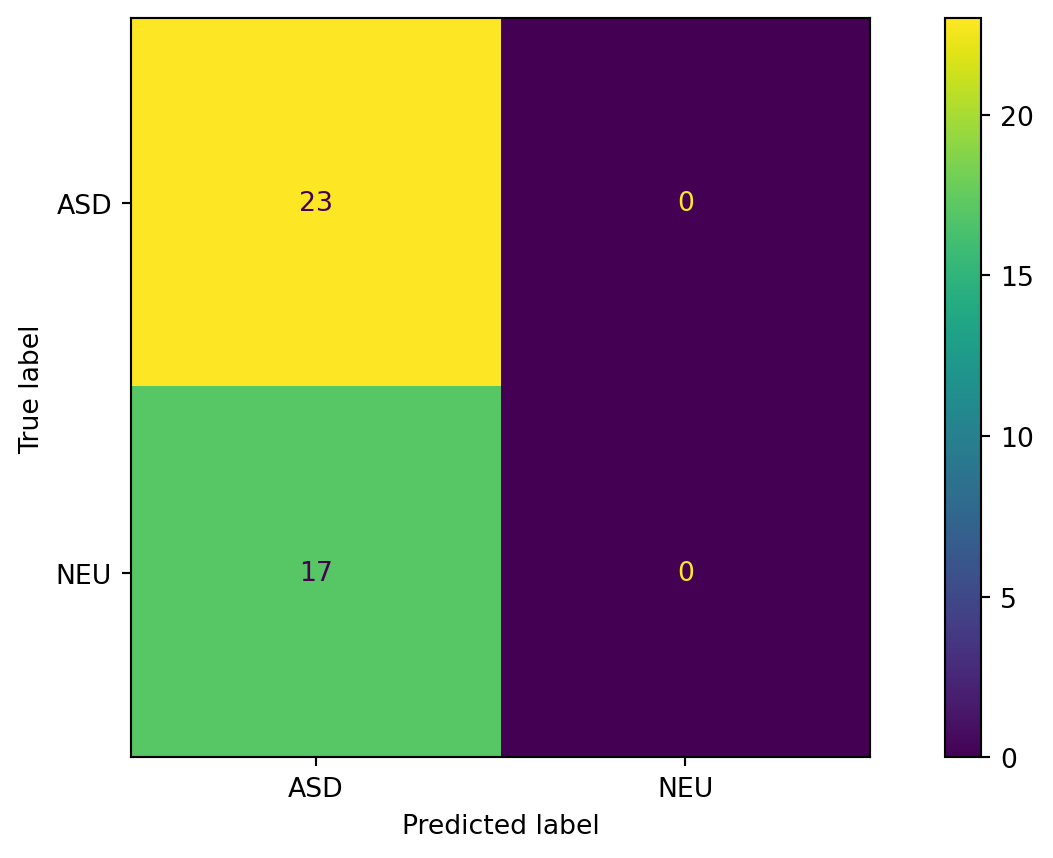
What if we always guessed the most common outcome?

from sklearn.dummy import DummyClassifier
most_common = DummyClassifier(strategy="most_frequent").fit(
    X=train[feature_columns],
    y=train[target_column]
)
test["pred_most_common"] = most_common.predict(test[feature_columns])
accuracy_score(test[target_column], test["pred_most_common"])
0.575

Confusion Matrix for most common

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
ConfusionMatrixDisplay.from_estimator(
    estimator=most_common,
    X=test[feature_columns],
    y=test[target_column],
    labels=[positive_outcome, negative_outcome]
)

Uniform Random Guess

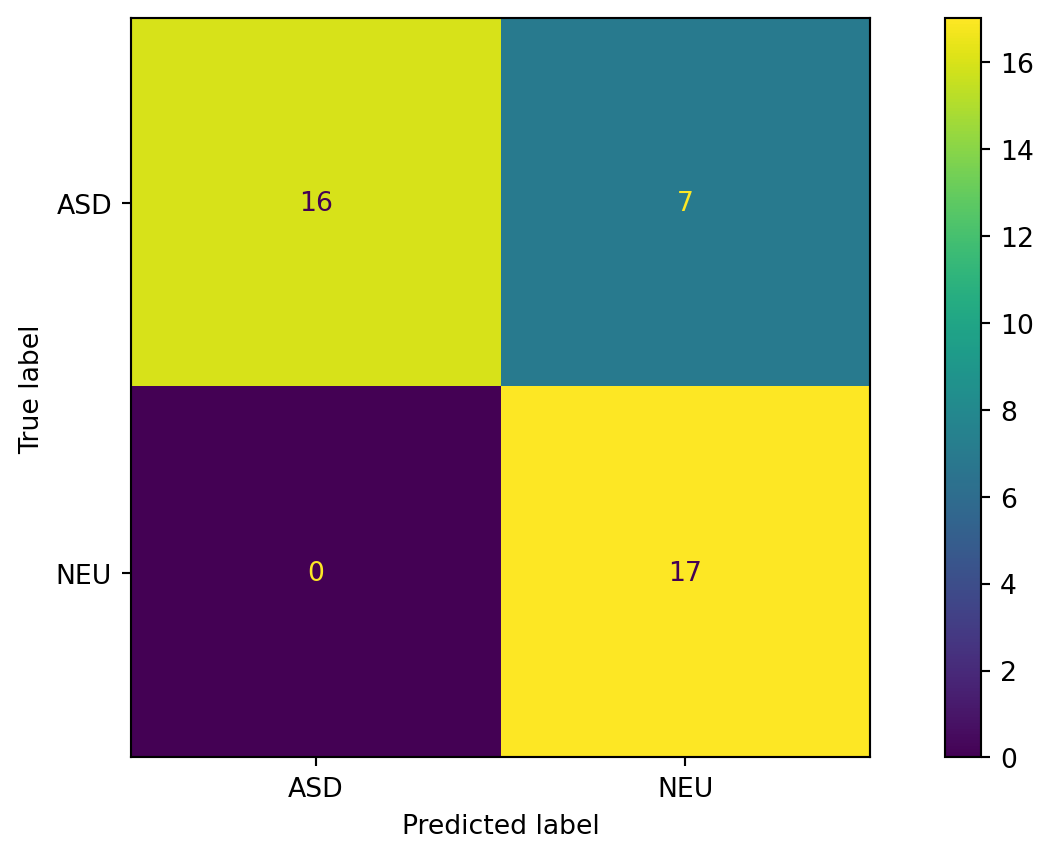
Or what if we guess uniformly at random?

uniform = DummyClassifier(strategy="uniform", random_state=0).fit(
    X=train[feature_columns],
    y=train[target_column]
)
test["pred_uniform"] = uniform.predict(test[feature_columns])
accuracy_score(test[target_column], test["pred_uniform"])
0.55

Confusion Matrix for Guessing Uniformly

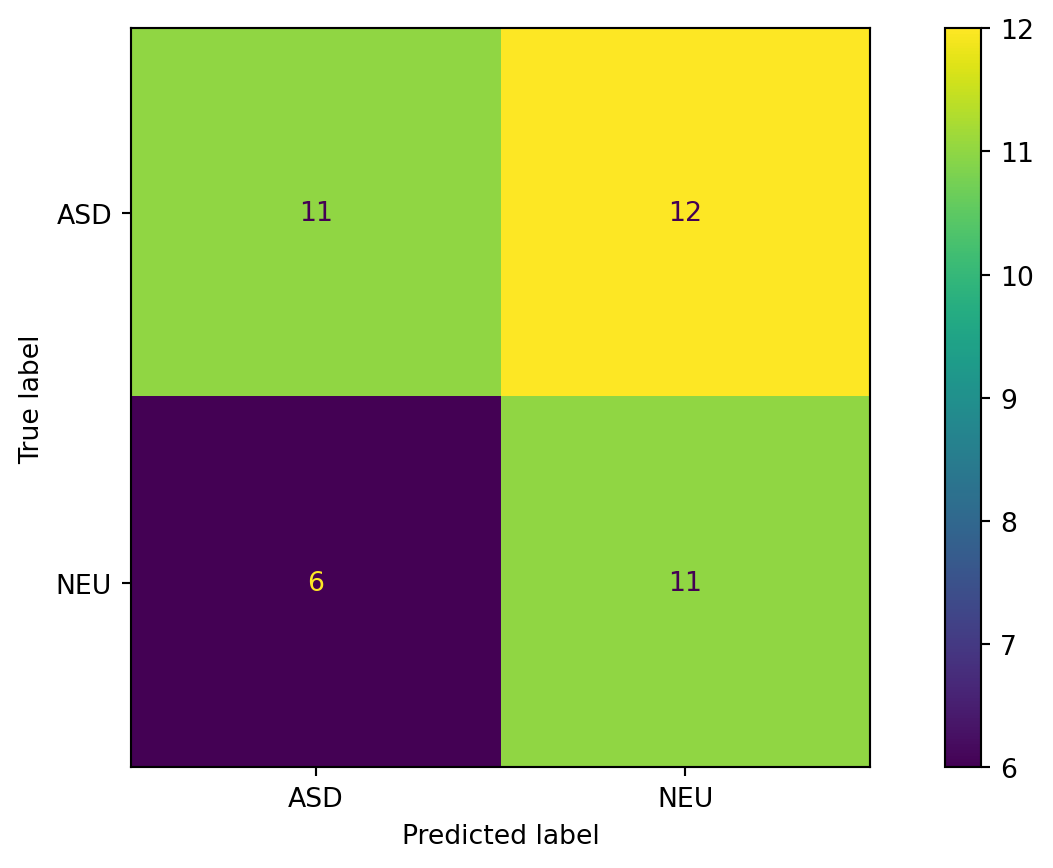
Exercise: compute the following for this classifier:

  • Accuracy
  • False positive rate
  • False negative rate
  • Sensitivity
  • Specificity
  • Precision
  • Recall

Computing these automatically

Now we can compute them (see docs on classification metrics)

from sklearn.metrics import classification_report
print(classification_report(
    y_true=test[target_column],
    y_pred=test["pred_uniform"],
))
              precision    recall  f1-score   support

         ASD       0.65      0.48      0.55        23
         NEU       0.48      0.65      0.55        17

    accuracy                           0.55        40
   macro avg       0.56      0.56      0.55        40
weighted avg       0.58      0.55      0.55        40

Let’s compute these quantities straight from the confusion matrix.

from sklearn.metrics import confusion_matrix
(tn, fp), (fn, tp) = confusion_matrix(
    y_true=test[target_column],
    y_pred=test["pred_uniform"],
    labels=[negative_outcome, positive_outcome]
)
num_positives = tp + fn
num_negatives = tn + fp
print(f"Accuracy: {(tp + tn) / (num_positives + num_negatives):.2f}")
print(f"False positive rate: {fp / num_negatives:.2f}")
print(f"False negative rate: {fn / num_positives:.2f}")
print(f"Sensitivity / recall: {tp / num_positives:.2f}")
print(f"Specificity: {tn / (tn + fp):.2f}")
print(f"Precision: {tp / (tp + fp):.2f}")
Accuracy: 0.55
False positive rate: 0.35
False negative rate: 0.52
Sensitivity / recall: 0.48
Specificity: 0.65
Precision: 0.65

Decision Tree

from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=1).fit(
    X=train[feature_columns],
    y=train[target_column]
)
train["pred_tree"] = tree.predict(train[feature_columns])
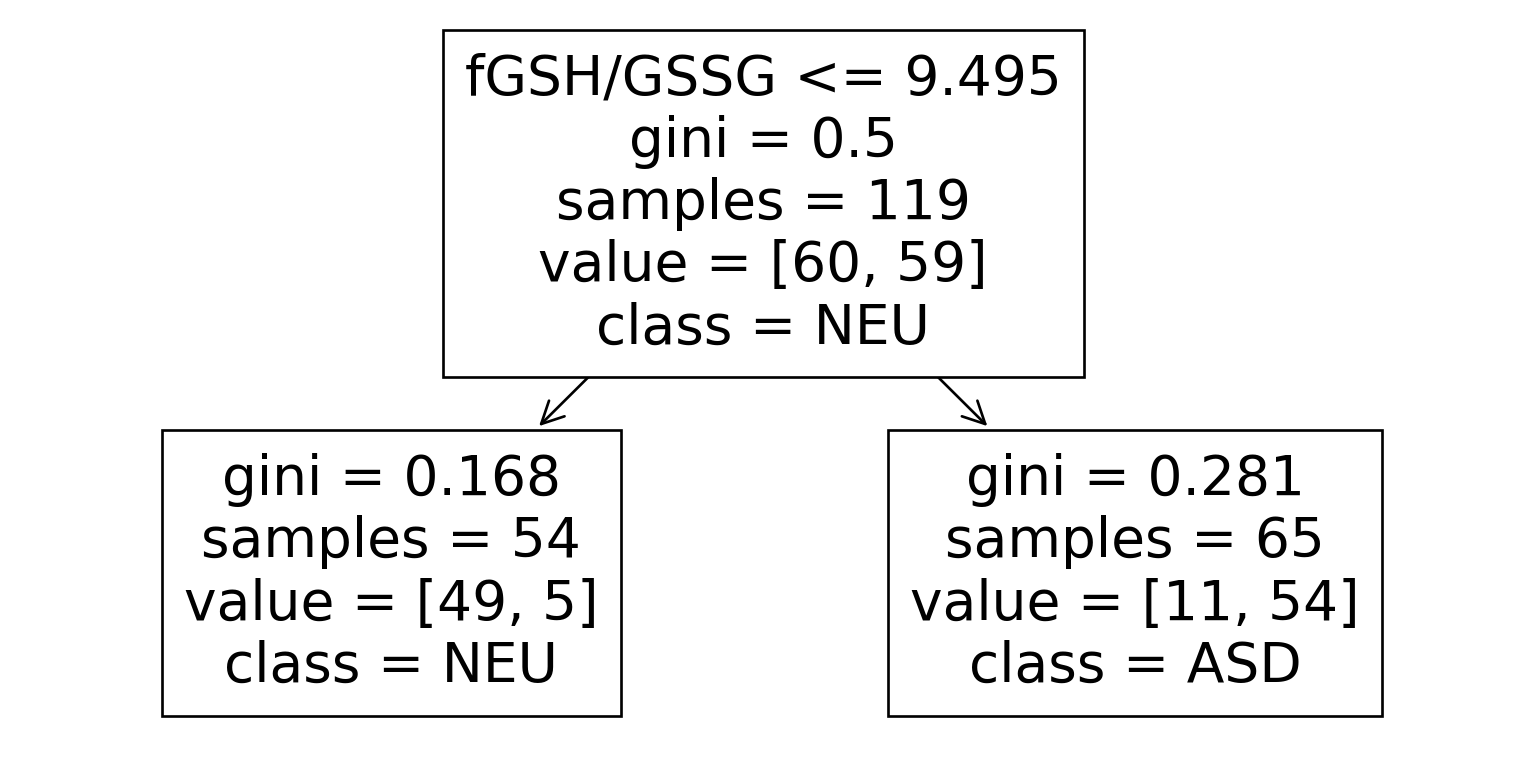
print("Training accuracy: ", accuracy_score(train[target_column], train["pred_tree"]))
Training accuracy:  0.865546218487395
test["pred_tree"] = tree.predict(test[feature_columns])
print("Test accuracy: ", accuracy_score(test[target_column], test["pred_tree"]))
Test accuracy:  0.825

Confusion Matrix

ConfusionMatrixDisplay.from_estimator(
    estimator=tree,
    X=test[feature_columns],
    y=test[target_column],
    labels=[positive_outcome, negative_outcome]
)

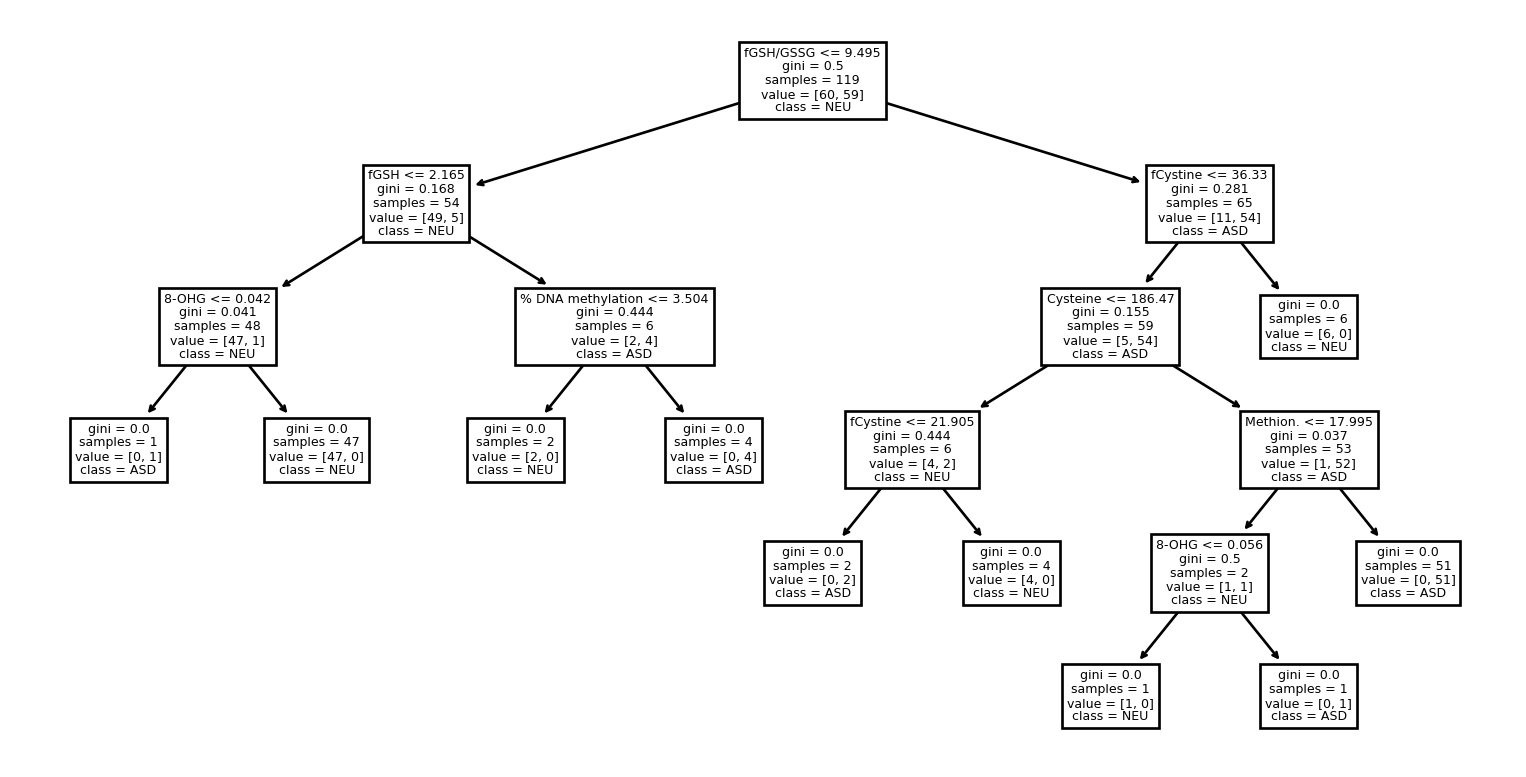
What does the tree look like?

from sklearn.tree import plot_tree
plot_tree(tree, feature_names=feature_columns, class_names=[negative_outcome, positive_outcome]);

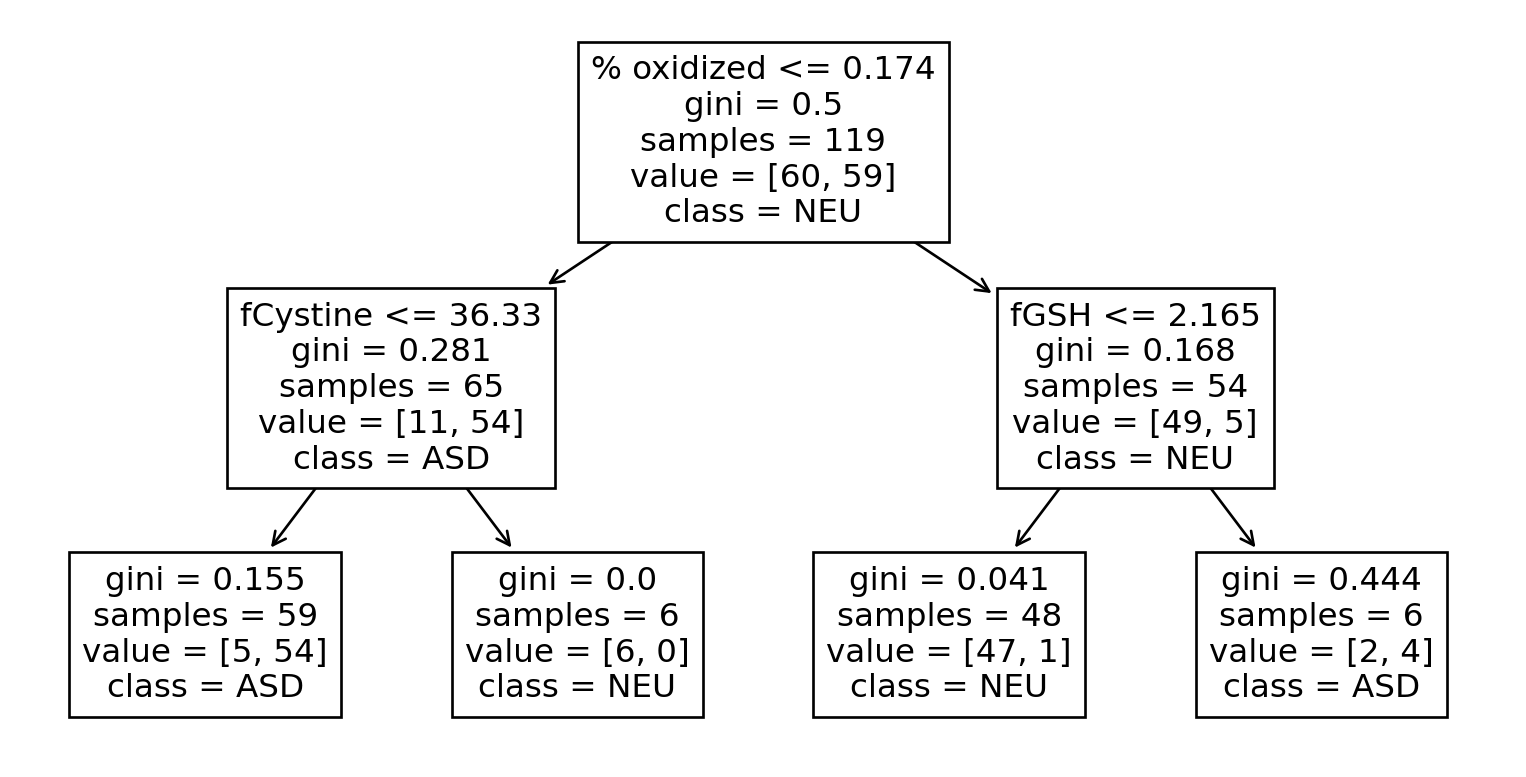
Go Deeper

tree = DecisionTreeClassifier(max_depth=2).fit(
    X=train[feature_columns],
    y=train[target_column]
)
train["pred_tree"] = tree.predict(train[feature_columns])
print("Training accuracy: ", accuracy_score(train[target_column], train["pred_tree"]))
Training accuracy:  0.9327731092436975
plot_tree(tree, feature_names=feature_columns, class_names=[negative_outcome, positive_outcome]);

test["pred_tree"] = tree.predict(test[feature_columns])
print("Test accuracy: ", accuracy_score(test[target_column], test["pred_tree"]))
Test accuracy:  0.875

Even Deeper

tree = DecisionTreeClassifier(max_depth=30).fit(
    X=train[feature_columns],
    y=train[target_column]
)
train["pred_tree"] = tree.predict(train[feature_columns])
print("Training accuracy: ", accuracy_score(train[target_column], train["pred_tree"]))
Training accuracy:  1.0
plot_tree(tree, feature_names=feature_columns, class_names=[negative_outcome, positive_outcome]);

What do you think the test accuracy will be?

test["pred_tree"] = tree.predict(test[feature_columns])
print("Test accuracy: ", accuracy_score(test[target_column], test["pred_tree"]))
Test accuracy:  0.85

What decisions can be made at each node

  • Continuous variables: compare one feature against a threshold value; if comparison is true go right, else go left
  • Categorical variables: if is one of a set of categories, go right, else left
  • At leaf nodes:
    • regression tree: compute the mean value of items there, predict that.
    • classification tree: compute the proportion of each category for items there
      • predict the most common category
      • or: predict that unseen items will follow the same proportions

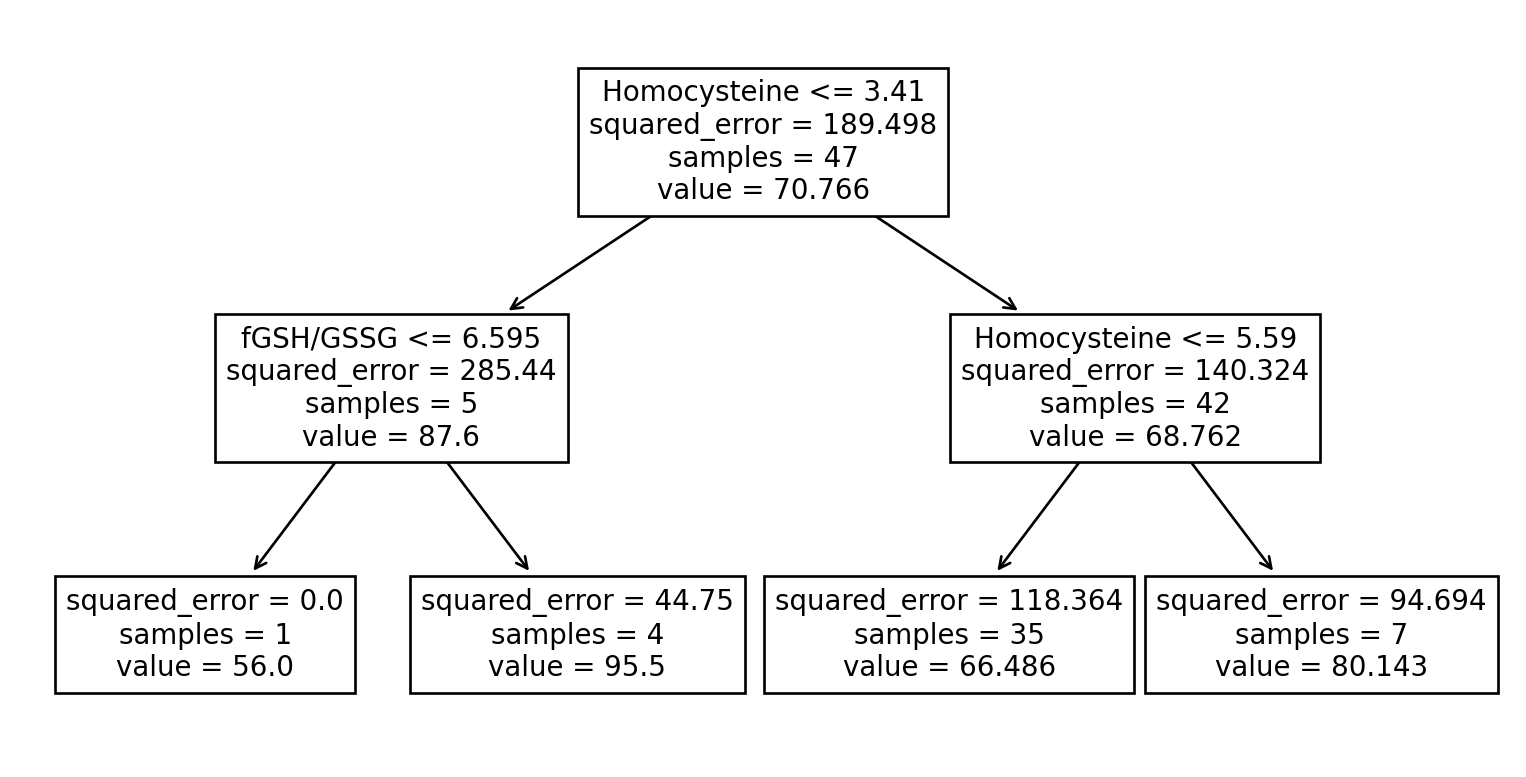
Example of a Regression Tree

We’ll try predicting the “Vineland ABC” score from the metabolites (for just the ASD children).

We’ll skip the usual train-test split because we’re just showing what the tree looks like.

from sklearn.tree import DecisionTreeRegressor
just_asd = autism.query("Group == 'ASD'").dropna().copy()
regression_tree = DecisionTreeRegressor(max_depth=2).fit(
    X=just_asd[feature_columns],
    y=just_asd["Vineland ABC"]
)

What a regression tree looks like

plot_tree(regression_tree, feature_names=feature_columns);

Activity

Training Data (Classification Tree)

Dataset 0

A D E
1734 Attchd No
1422 Attchd Yes
1464 Attchd Yes
2320 Detchd Yes
2290 Detchd No
1969 Detchd No

Dataset 1

B C E
1973 Twnhs No
1980 Duplex No
2002 OneFam Yes
1962 OneFam No
1994 OneFam Yes
1994 OneFam Yes

Dataset 2

A C E
1367 TwnhsE Yes
1512 OneFam Yes
1149 OneFam No
796 OneFam No
1264 OneFam Yes
1314 OneFam No

Dataset 3

A C E
932 OneFam No
1242 OneFam Yes
1668 OneFam No
1092 TwoFmCon No
1226 TwnhsE Yes
2418 OneFam Yes

Dataset 4

A C E
864 OneFam No
1434 OneFam No
1196 OneFam No
1720 OneFam Yes
2787 Duplex Yes
1586 Twnhs Yes

Dataset 5

B D E
1900 Detchd No
2006 Attchd Yes
1929 Detchd Yes
1940 Detchd No
1970 Attchd Yes
1916 Detchd No

Dataset 6

B C E
2000 OneFam Yes
1967 OneFam No
1974 OneFam Yes
1997 OneFam Yes
1956 OneFam No
1948 OneFam No

Dataset 7

B C E
2005 OneFam Yes
1950 OneFam Yes
1937 OneFam No
1915 OneFam No
1980 OneFam Yes
1971 OneFam No

Dataset 8

A C E
1403 OneFam Yes
1342 OneFam No
2161 OneFam Yes
1092 Twnhs No
1852 OneFam Yes
1578 OneFam No

Dataset 9

B C E
1959 OneFam Yes
1914 OneFam No
1931 OneFam Yes
2001 OneFam Yes
1930 OneFam No
1936 OneFam No

Test set

A B C D
1502 1923 OneFam Detchd
1561 1960 OneFam Attchd
2650 1967 Duplex Other
1328 1959 OneFam Attchd
3228 1992 OneFam Attchd
1774 1900 OneFam Other

Training Data (Regression Tree)

Dataset 0

A D F
1734 Attchd 126.0
1422 Attchd 179.6
1464 Attchd 282.9
2320 Detchd 259.5
2290 Detchd 122.5
1969 Detchd 141.0

Dataset 1

B C F
1973 Twnhs 119.5
1980 Duplex 144.0
2002 OneFam 220.0
1962 OneFam 130.0
1994 OneFam 193.5
1994 OneFam 301.5

Dataset 2

A C F
1367 TwnhsE 192.0
1512 OneFam 231.0
1149 OneFam 127.0
796 OneFam 85.0
1264 OneFam 167.5
1314 OneFam 145.0

Dataset 3

A C F
932 OneFam 124.0
1242 OneFam 175.5
1668 OneFam 135.0
1092 TwoFmCon 55.0
1226 TwnhsE 211.5
2418 OneFam 341.0

Dataset 4

A C F
864 OneFam 133.5
1434 OneFam 157.0
1196 OneFam 128.0
1720 OneFam 188.0
2787 Duplex 269.5
1586 Twnhs 170.0

Dataset 5

B D F
1900 Detchd 114.0
2006 Attchd 325.0
1929 Detchd 230.0
1940 Detchd 155.0
1970 Attchd 240.1
1916 Detchd 135.0

Dataset 6

B C F
2000 OneFam 327.0
1967 OneFam 134.5
1974 OneFam 260.0
1997 OneFam 210.0
1956 OneFam 131.0
1948 OneFam 138.0

Dataset 7

B C F
2005 OneFam 415.0
1950 OneFam 257.0
1937 OneFam 119.5
1915 OneFam 123.0
1980 OneFam 204.0
1971 OneFam 119.5

Dataset 8

A C F
1403 OneFam 202.0
1342 OneFam 105.0
2161 OneFam 230.5
1092 Twnhs 85.5
1852 OneFam 230.0
1578 OneFam 133.0

Dataset 9

B C F
1959 OneFam 200.0
1914 OneFam 67.0
1931 OneFam 169.5
2001 OneFam 421.2
1930 OneFam 110.0
1936 OneFam 115.0

Test set

A B C D
1502 1923 OneFam Detchd
1561 1960 OneFam Attchd
2650 1967 Duplex Other
1328 1959 OneFam Attchd
3228 1992 OneFam Attchd
1774 1900 OneFam Other

Instructions

Columns A through D are features. Columns E and F are outcomes (targets).

  1. Pick a random number between 0 and 9 (inclusive). This is your dataset number.
  2. On paper, construct a decision tree to predict E from the features in your dataset.
    • This doesn’t have to be the best possible tree; just try to come up with some reasonable tree.
  3. Make a second tree to predict F from the features in your dataset.
  4. Compute the accuracy and MAE of your tree on your training set.
  5. Write down what your tree predicts for both E and F for each item in the test set.

Don’t peek beyond this slide until you’re done!

Evaluation

Here’s the test set with labels:

Gr_Liv_Area Year_Built Bldg_Type Garage_Type sale_price_above_median sale_price
1502 1923 OneFam Detchd Yes 165.000000
1561 1960 OneFam Attchd Yes 193.000000
2650 1967 Duplex Other Yes 160.000000
1328 1959 OneFam Attchd Yes 170.000000
3228 1992 OneFam Attchd Yes 430.000000
1774 1900 OneFam Other No 87.000000

Compute your accuracy and MAE.

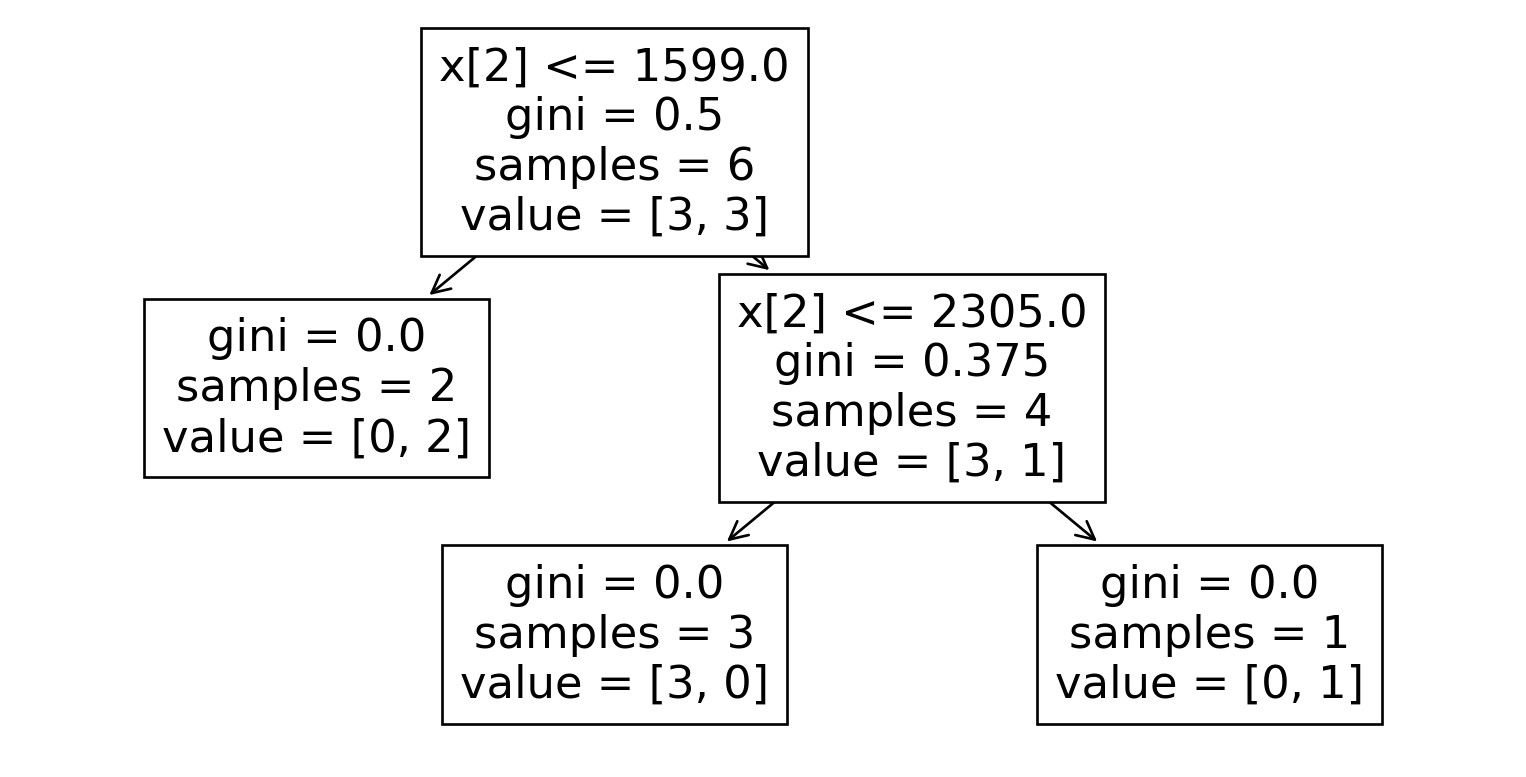
Reference Results

Here’s what classification trees look like for each dataset:

Dataset 0

A D E
1734 Attchd No
1422 Attchd Yes
1464 Attchd Yes
2320 Detchd Yes
2290 Detchd No
1969 Detchd No

Dataset 1

B C E
1973 Twnhs No
1980 Duplex No
2002 OneFam Yes
1962 OneFam No
1994 OneFam Yes
1994 OneFam Yes

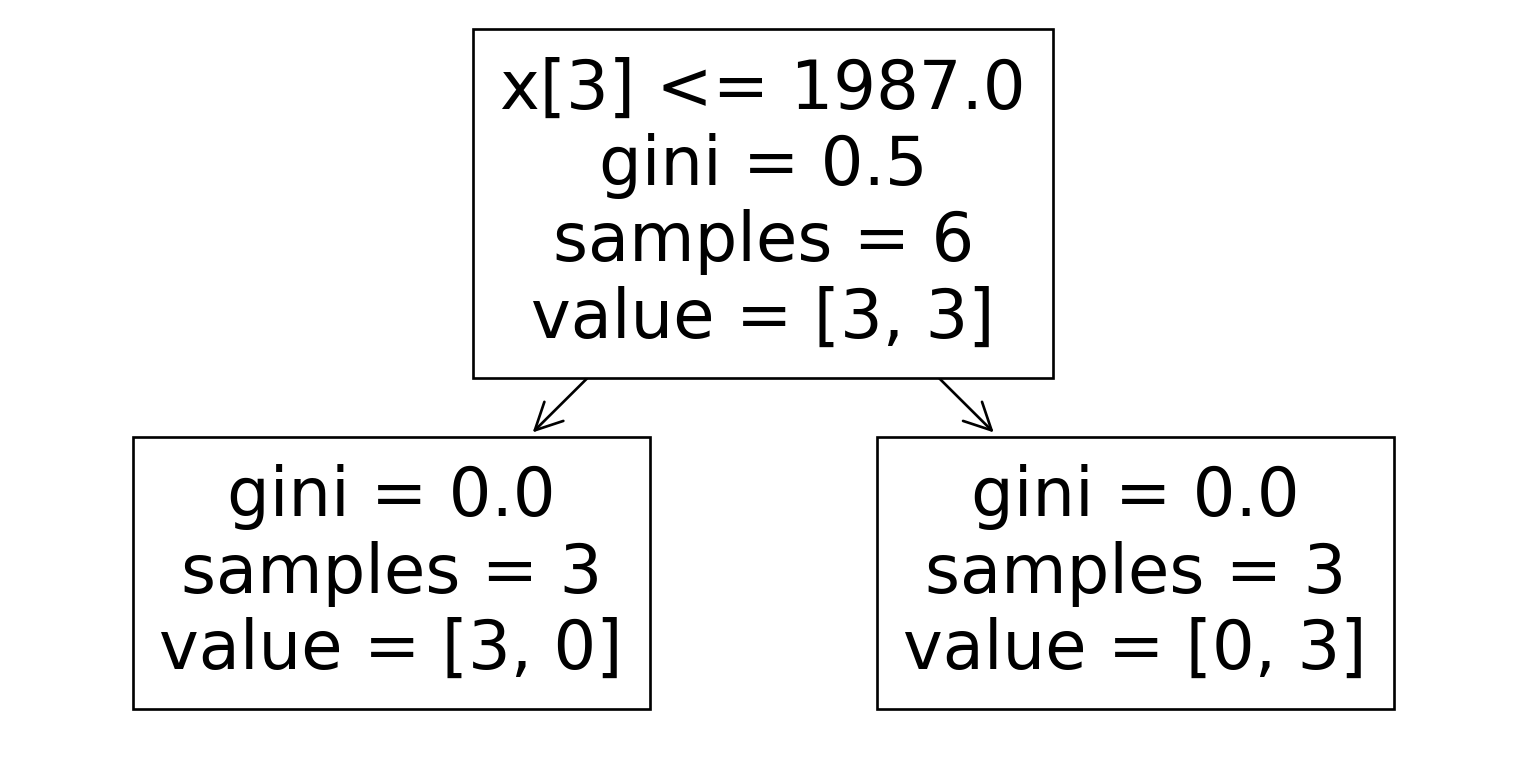
Dataset 2

A C E
1367 TwnhsE Yes
1512 OneFam Yes
1149 OneFam No
796 OneFam No
1264 OneFam Yes
1314 OneFam No

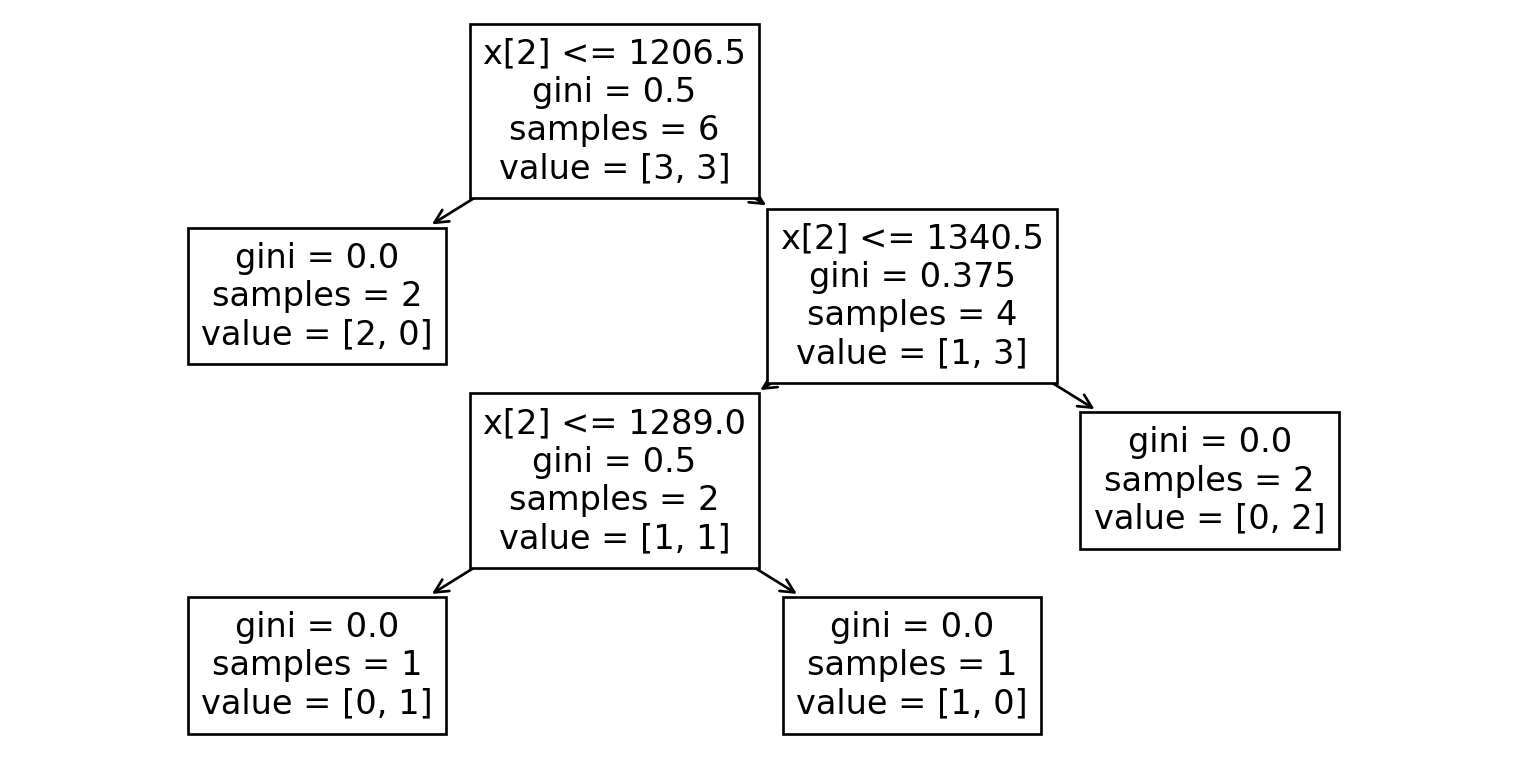
Dataset 3

A C E
932 OneFam No
1242 OneFam Yes
1668 OneFam No
1092 TwoFmCon No
1226 TwnhsE Yes
2418 OneFam Yes

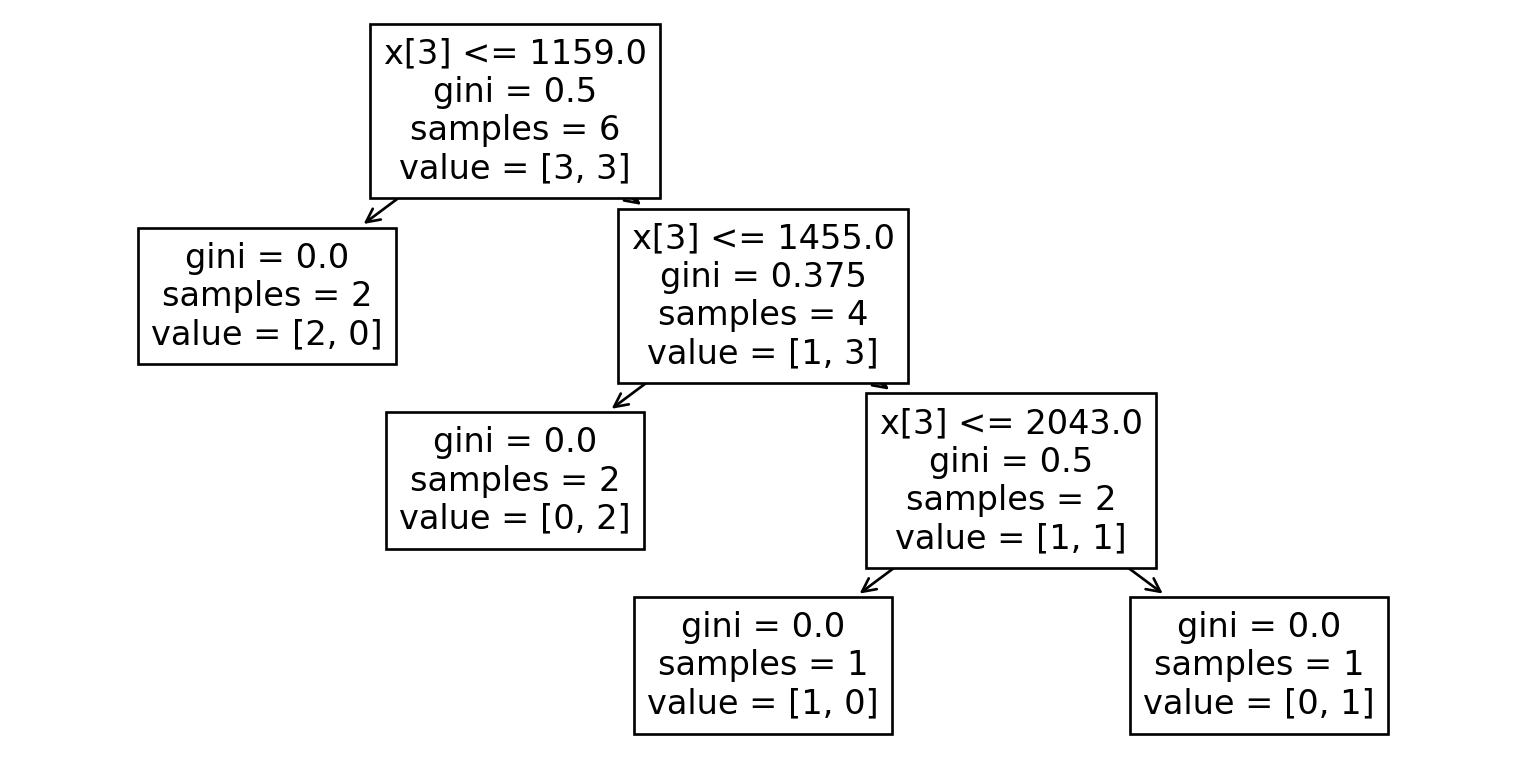
Dataset 4

A C E
864 OneFam No
1434 OneFam No
1196 OneFam No
1720 OneFam Yes
2787 Duplex Yes
1586 Twnhs Yes

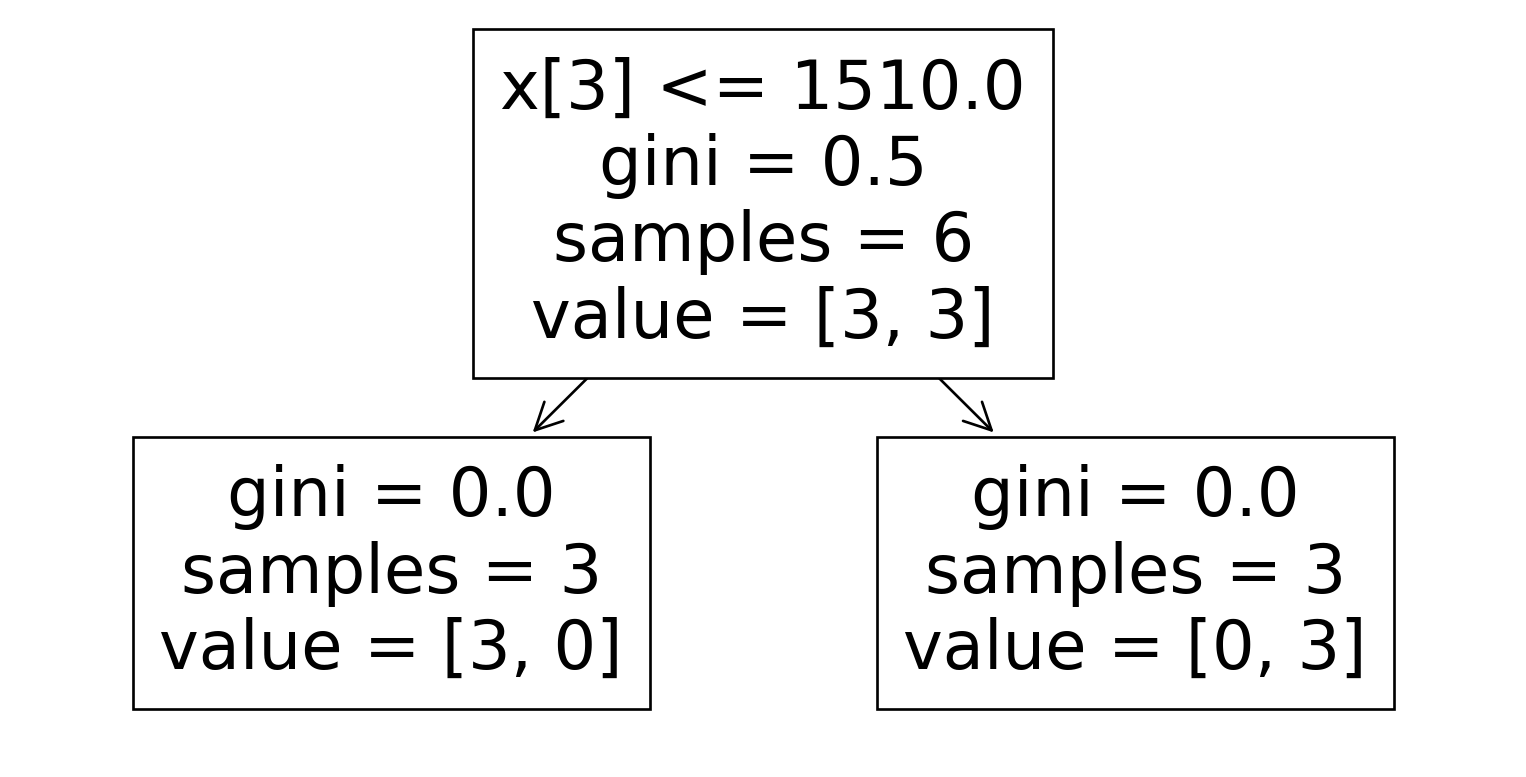
Dataset 5

B D E
1900 Detchd No
2006 Attchd Yes
1929 Detchd Yes
1940 Detchd No
1970 Attchd Yes
1916 Detchd No

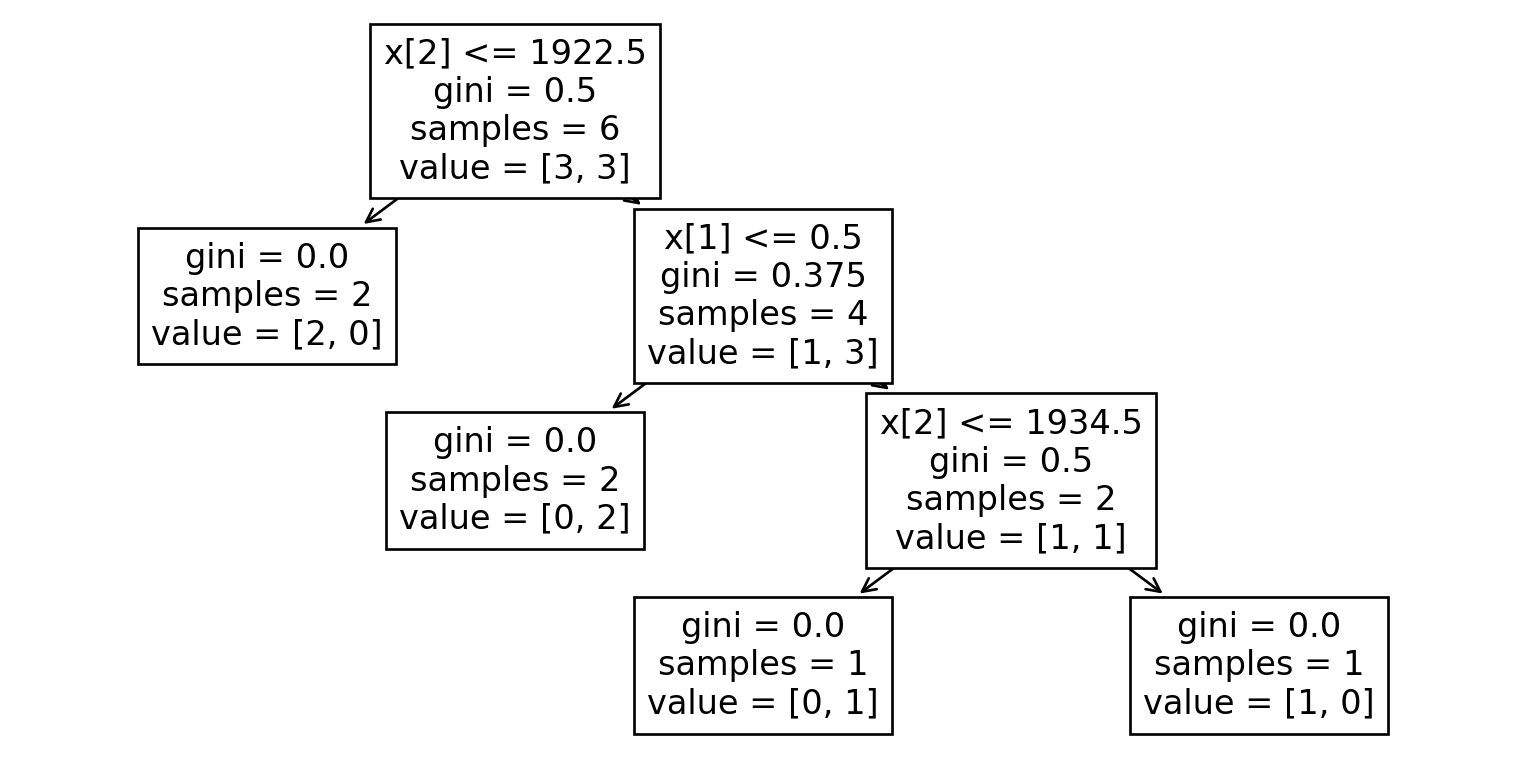
Dataset 6

B C E
2000 OneFam Yes
1967 OneFam No
1974 OneFam Yes
1997 OneFam Yes
1956 OneFam No
1948 OneFam No

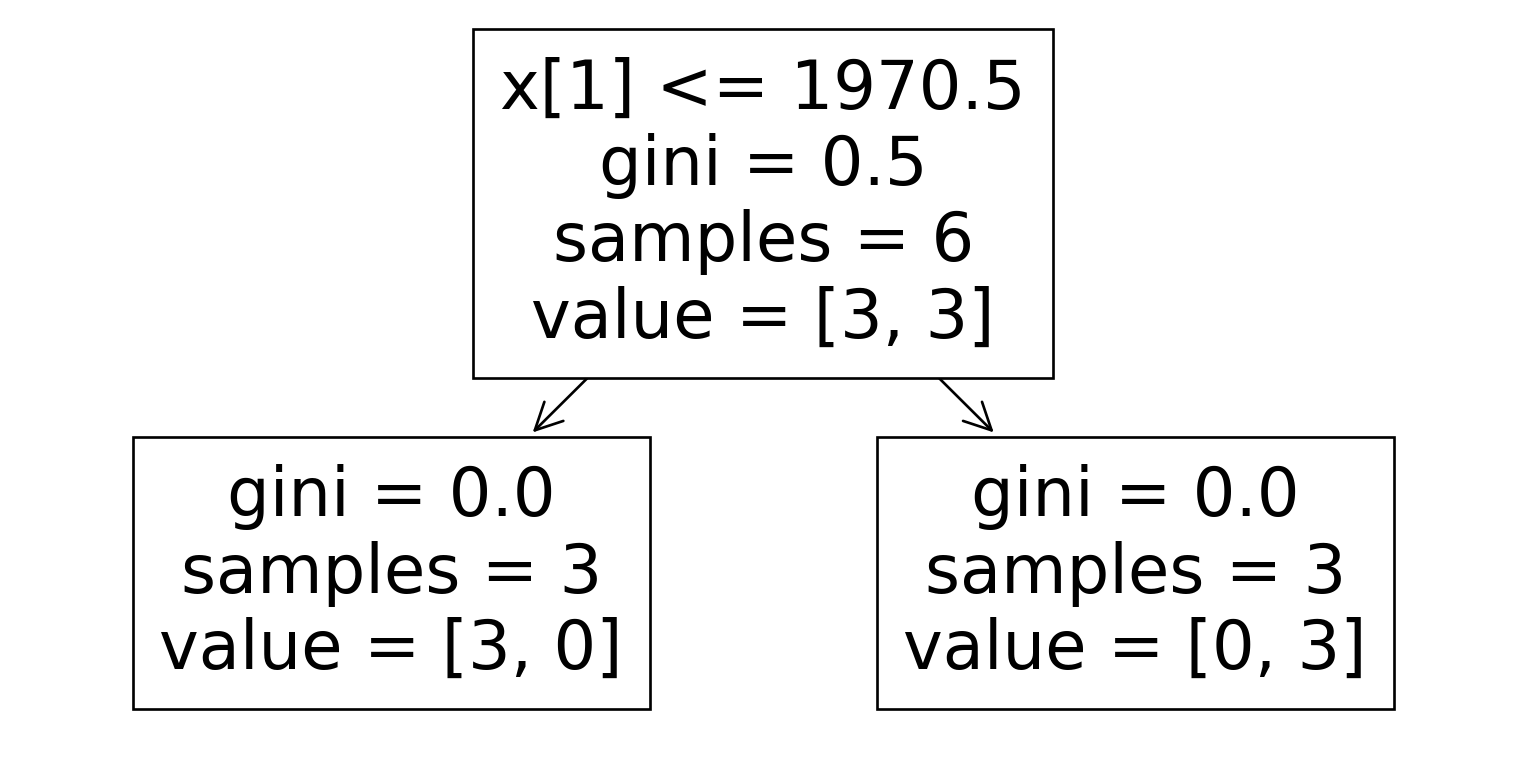
Dataset 7

B C E
2005 OneFam Yes
1950 OneFam Yes
1937 OneFam No
1915 OneFam No
1980 OneFam Yes
1971 OneFam No

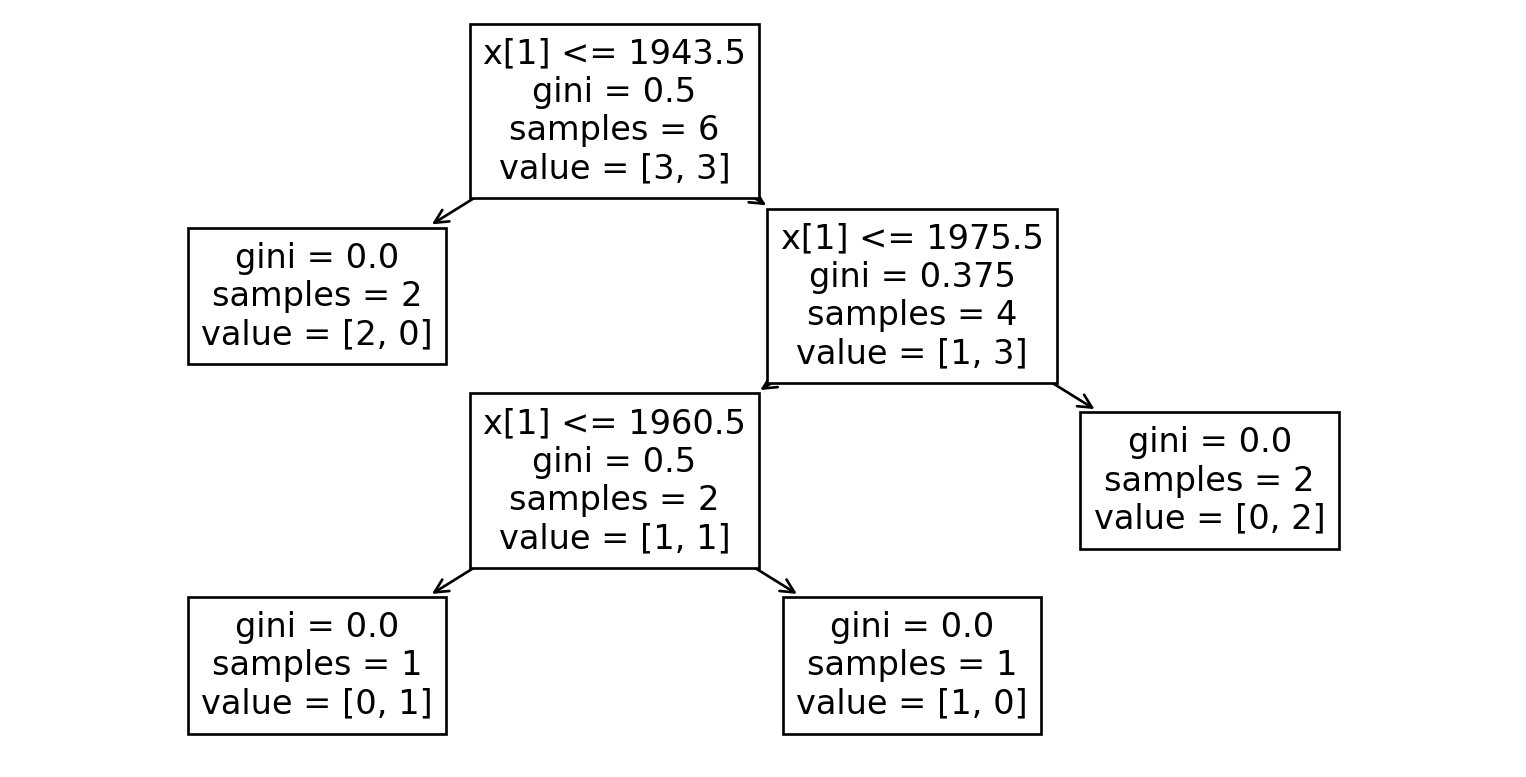
Dataset 8

A C E
1403 OneFam Yes
1342 OneFam No
2161 OneFam Yes
1092 Twnhs No
1852 OneFam Yes
1578 OneFam No

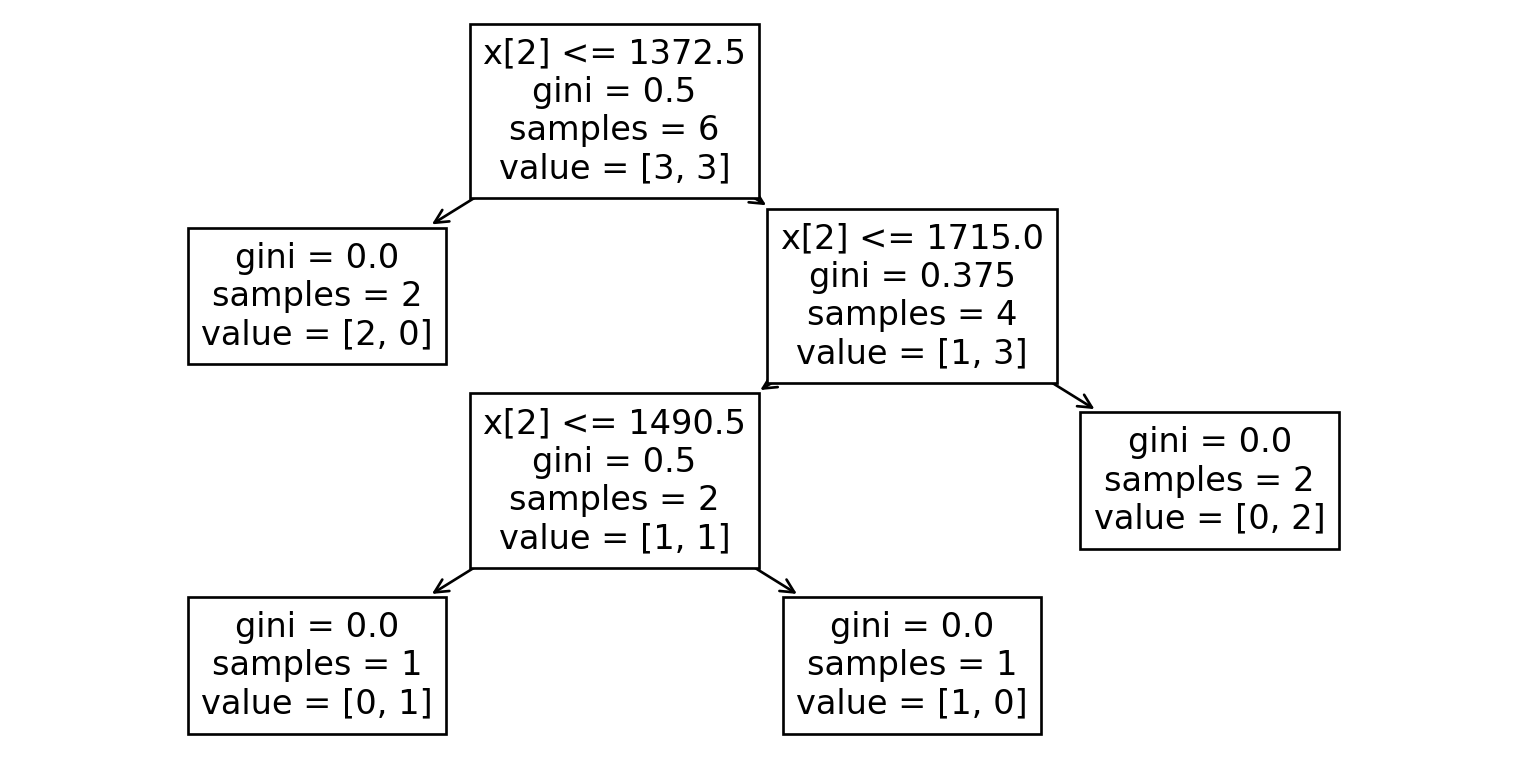
Dataset 9

B C E
1959 OneFam Yes
1914 OneFam No
1931 OneFam Yes
2001 OneFam Yes
1930 OneFam No
1936 OneFam No

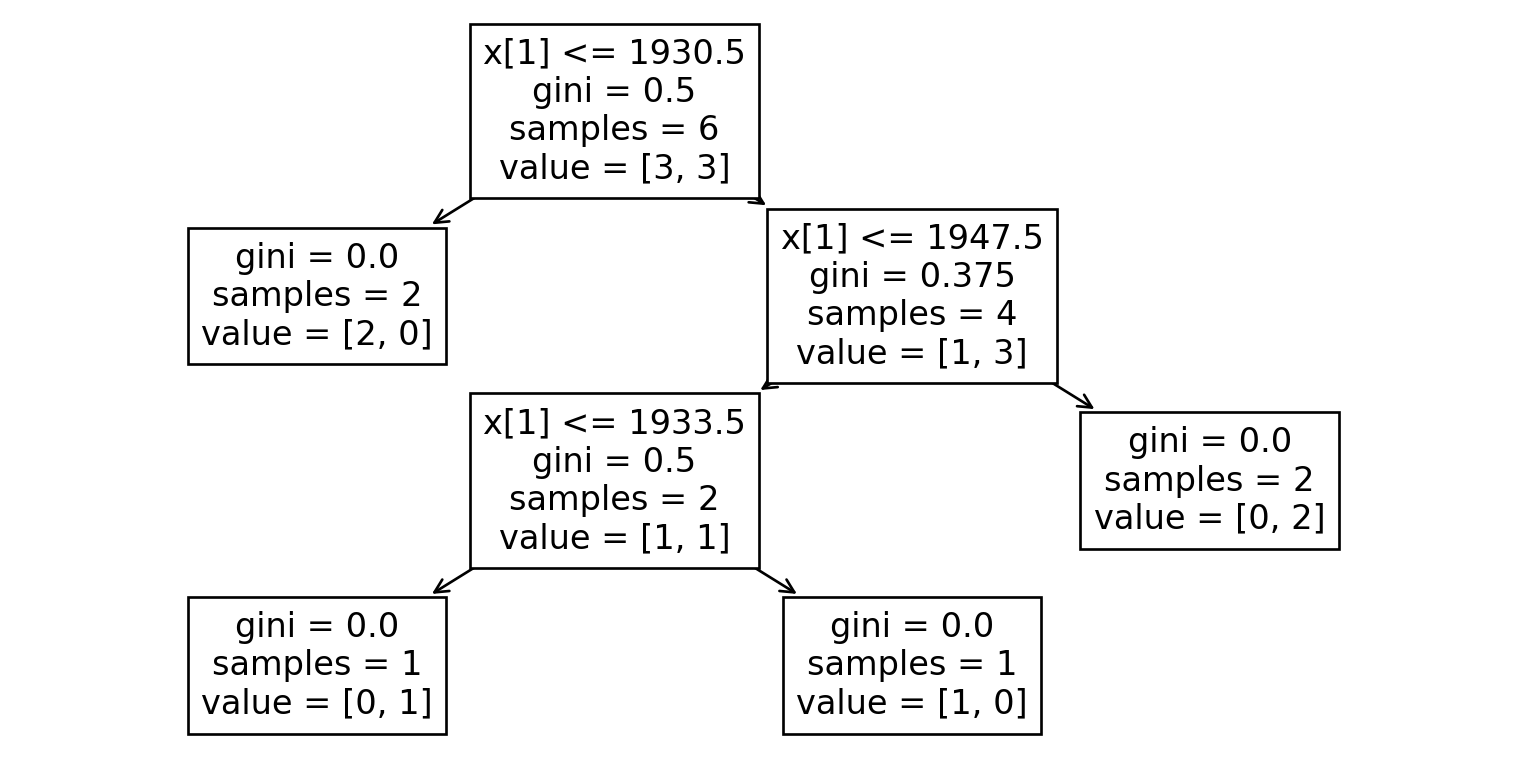
Test set

Gr_Liv_Area Year_Built Bldg_Type Garage_Type yes_votes sale_price_above_median Tree 1 Tree 2 Tree 3 Tree 4 Tree 5 Tree 6 Tree 7 Tree 8 Tree 9 Tree 10
1502 1923 OneFam Detchd 0.300000 Yes Yes No Yes No No Yes No No No No
1561 1960 OneFam Attchd 0.600000 Yes Yes No Yes No Yes Yes No Yes No Yes
2650 1967 Duplex Other 0.700000 Yes Yes No Yes Yes Yes Yes No No Yes Yes
1328 1959 OneFam Attchd 0.500000 Yes Yes No No Yes No Yes No Yes No Yes
3228 1992 OneFam Attchd 1.000000 Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes Yes
1774 1900 OneFam Other 0.300000 No No No Yes No Yes No No No Yes No