Bayesian Networks: a short introduction
Probabilistic Predictions
- What if we don’t want just a prediction, but also to know how certain our model is about that prediction?
- For example, “given our model, we are 70% certain that it could be one disease, 20% it could be another, and 10% another”.
- Let’s use statistics! Starting with categorical variables…
- Say we have variables \(A, B, C\).
- \(A\) can assume values \(a^0\) and \(a^1\), \(B\) can assume \(b^0\) and \(b^1\), and so on.
- Question: we want to know probabilities on \(D\) having values \(d^0\) or \(d^1\) given we know values about \(A, B\) and \(C\).
- For example, \(P(d^0 | a^0, b^1, c^1)\) and \(P(d^1 | a^0, b^1, c^1)\). (Note that these would sum to \(1\)).
- \(D\) is our target, \(A,B,C\) are our features!
Bayesian statistics
- At some point we would probably need a joint probability distribution: \(P(A, B, C, D)\)
- Then, we calculate \(P(D | A, B, C) = \frac{P(A, B, C, D)}{P(A, B, C)}\)
- We get \(P(A, B, C)\) from marginalization:
\[ P(A,B,C) = \sum_{D}P(A,B,C,D)=P(A,B,C,d^0)+P(A,B,C,d^1) \]
- However, how to obtain \(P(A, B, C, D)\)?
- 4 variables with 2 values each: \(2^4\) = 16 cells
- One way: just consult an expert and come up with the numbers
- But… can we estimate these probabilities from data? How much samples would we need?
Probabilistic Graphical Models
Maybe we can use a graphical representation that helps us simplify that probability?
Several options: Markov Hidden Models, Bayesian networks…
Bayesian networks take advantage on the conditional independence of the variables…

Statistical independence
- Variables \(A\) and \(B\) are independent (\(A⊥B\)) if:
- \(P(A,B)=P(A)P(B)\)
- Which also means: \(P(A | B) = P(A)\) and \(P(B | A) = P(B)\)
- Now, variables can be conditionally independent. \(A\) and \(B\) are said to be independent *given that** I already know some value of a third variable \(C\) (\(A⊥B|C\)):
- \(P(A,B|C)=P(A|C)P(B|C)\)
- Which also means: \(P(A | B, C) = P(A | C)\) and \(P(B | A, C) = P(B | C)\)
- And: \(P(A,B,C)=P(A,B|C)P(C)=P(A|C)P(B|C)P(C)\)
An example
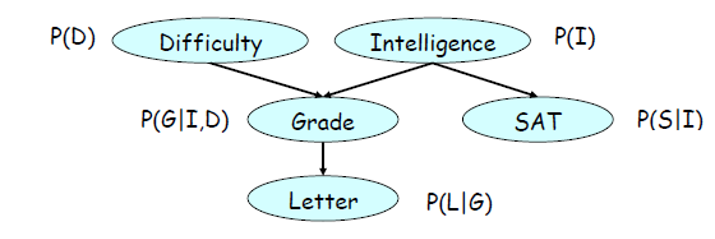
- Difficulty \(D\) is clearly independent of Intelligence \(I\).
- If I already know Intelligence \(I\), knowing the Grade \(G\) wouldn’t add anything to knowing SAT \(S\). It is “independent”.
- But, if I don’t know Intelligence \(I\), knowing the Grade \(G\) would really help knowing something about SAT. So, it is “dependent”.
- So, \(S⊥G|I\), in other words, \(S\) is independent of \(G\) on the condition of knowing \(I\).
Bayesian Networks
- Represent the relationship between variables in terms of conditional independencies
- “Kind of” conveys the idea of how one variable causally influences another, but not always (causality is a complex and disputed notion)
- This is done with a directed acyclic graph (DAG) representation
- Every node has attributed to it a probability distribution conditioned on its parent nodes
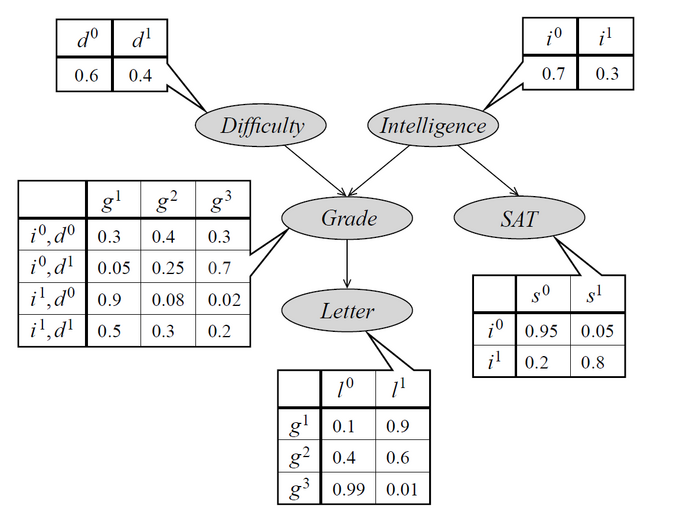
- What is most interesting about that is the possibility to decompose the joint probability distribution. For example:
\[ P(D,I,G,S,L) = P(D)P(I)P(G|I,D)P(S|I)P(L|G) \]
- Why is this good? Each distribution can (in principle) be elaborated or trained separately!
- However, we also need to be sure about the conditional independencies
Inferences
- What’s the probability of a recommendation letter given that a student’s SAT is \(s^0\)?
- This means obtaining \(P(L|s^0)\) through the variable elimination algorithm

\[ P(L|s^0) = \frac{P(L,s^0)}{P(s^0)} = \sum_{D,I,G}\frac{P(D,I,G,L,s^0)}{P(s^0)} \] Applying the BN decomposition:
\[ P(L|s^0)= \frac{1}{P(s^0)}\sum_{D,I,G}P(D)P(I)P(G|I,D)P(s^0|I)P(L|G) \]
Calculating \(P(s^0)\):
\[ P(s^0) = \sum_{I}P(s^0,I) = \sum_{I}P(s^0|I)P(I) = P(s^0|i^0)P(i^0) + P(s^0|i^1)P(i^1) = 0.95\times0.7 + 0.2\times0.3 \]
Now, back to \(P(L|s^0)\), let’s eliminate variable \(D\):
\[ P(L|s^0)=\frac{1}{P(s^0)}\sum_{I,G}P(I)P(s^0|I)P(L|G)\sum_{D}P(D)P(G|I,D) \]
This gives us a table \(\tau_1(G,I)=\sum_{D}P(D)P(G|I,D)\)
Now, we eliminate \(I\):
\[ P(L|s^0) = \frac{1}{P(s^0)}\sum_{G}P(L|G)\sum_{I}P(s^0|I)P(I)\tau_1(G,I) \]
which gives us a table \(\tau_2(G)=\sum_{I}P(s^0|I)P(I)\tau_1(G,I)\)
Finally, we eliminate \(G\):
\[ P(L|s^0) = \frac{1}{P(s^0)}\sum_{G}P(L|G)\tau_2(G) \]
We thus get two numbers, \(P(L=l^0|s^0)\) and \(P(L=L=l^1|s^0)\), which would indicate the probability of each outcome.
BNs in Python
- A nice example is implemented with the sorobn library
Learning Bayesian Networks
How to use data to fit a Bayesian network? Two tasks:
- Learning the network structure
- Learning the conditional distribution parameters
Sometimes we mix a specialist knowledge with data, using a Bayesian learning approach
For example, what is the most probable graph \(G\) given we have dataset \(D\)? Bayes’ theorem:
\[ P(G|D)=\frac{P(D|G)P(G)}{P(D)} \propto P(D|G)P(G) \] * \(P(D|G\) can be calculated by exploring different network structures (likelihood of the data given a structure), and \(P(G)\) is called the a priori and is a specialist knowledge (for example, certain structures may be attributed a greater probability given what we expect).